Объем правильной шестиугольной пирамиды 6. Формула объема шестиугольной пирамиды: пример решения задачи

Формула объема шестиугольной пирамиды: пример решения задачи

Вычисление объемов пространственных фигур является одной из важных задач стереометрии. В данной статье рассмотрим вопрос определения объема такого полиэдра, как пирамида, а также приведем формулу объема пирамиды шестиугольной правильной.

Пирамида шестиугольная

Для начала рассмотрим, что собой представляет фигура, о которой пойдет речь в статье.

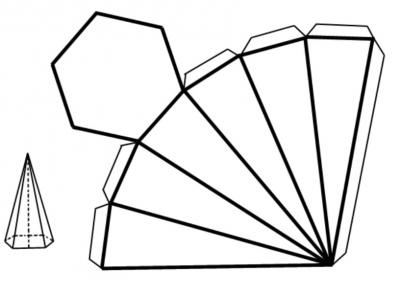
Пусть у нас имеется произвольный шестиугольник, стороны которого не обязательно равны друг другу. Также предположим, что мы выбрали в пространстве точку, не находящуюся в плоскости шестиугольника. Соединив все углы последнего с выбранной точкой, мы получим пирамиду. Две разные пирамиды, имеющие шестиугольное основание, показаны на рисунке ниже.

Видно, что помимо шестиугольника фигура состоит из шести треугольников, точка соединения которых называется вершиной. Различие между изображенными пирамидами заключается в том, что высота h правой из них не пересекает шестиугольное основание в его геометрическом центре, а высота левой фигуры попадает точно в этот центр. Благодаря этому критерию левая пирамида получила название прямой, а правая – наклонной.

Поскольку основание левой фигуры на рисунке образовано шестиугольником с равными сторонами и углами, то она называется правильной. Дальше в статье речь пойдет только об этой пирамиде.

Объем шестиугольной пирамиды

Для вычисления объема произвольной пирамиды справедлива следующая формула:

Здесь h – это длина высоты фигуры, S_o – площадь ее основания. Воспользуемся этим выражением для определения объема пирамиды шестиугольной правильной.

Поскольку в основании рассматриваемой фигуры лежит равносторонний шестиугольник, то для вычисления его площади можно воспользоваться следующим общим выражением для n-угольника:

S_n = n/4 * a 2 * ctg(pi/n)

Здесь n – целое число, равное количеству сторон (углов) многоугольника, a – длина его стороны, функцию котангенса высчитывают, используя соответствующие таблицы.

Применяя выражение для n = 6, получим:

S₆ = 6/4 * a 2 * ctg(pi/6) = √3/2 * a 2

Теперь остается подставить это выражение в общую формулу для объема V:

Таким образом, для вычисления объема рассматриваемой пирамиды необходимо знать два ее линейных параметра: длину стороны основания и высоту фигуры.

Пример решения задачи

Покажем, как можно использовать полученное выражение для V₆ для решения следующей задачи.

Известно, что правильной шестиугольной пирамиды объем равен 100 см 3 . Необходимо определить сторону основания и высоту фигуры, если известно, что они связаны друг с другом следующим равенством:

Поскольку в формулу для объема входят только a и h, то можно подставить в нее любой из этих параметров, выраженный через другой. Например, подставим a, получаем:

Для нахождения значения высоты фигуры необходимо взять корень третей степени из объема, что соответствует размерности длины. Подставляем значение объема V₆ пирамиды из условия задачи, получаем высоту:

h = ∛(100/(2*√3)) ≈ 3,0676 см

Поскольку сторона основания в соответствии с условием задачи в два раза больше найденной величины, то получаем значение для нее:

a = 2*h = 2*3,0676 = 6,1352 см

Объем шестиугольной пирамиды можно найти не только через высоту фигуры и значение стороны ее основания. Достаточно знать два разных линейных параметра пирамиды для его вычисления, например апотему и длину бокового ребра.

Формула объема шестиугольной пирамиды: пример решения задачи

Вычисление объемов пространственных фигур является одной из важных задач стереометрии. В данной статье рассмотрим вопрос определения объема такого полиэдра, как пирамида, а также приведем формулу объема пирамиды шестиугольной правильной.

Пирамида шестиугольная

Для начала рассмотрим, что собой представляет фигура, о которой пойдет речь в статье.

Пусть у нас имеется произвольный шестиугольник, стороны которого не обязательно равны друг другу. Также предположим, что мы выбрали в пространстве точку, не находящуюся в плоскости шестиугольника. Соединив все углы последнего с выбранной точкой, мы получим пирамиду. Две разные пирамиды, имеющие шестиугольное основание, показаны на рисунке ниже.

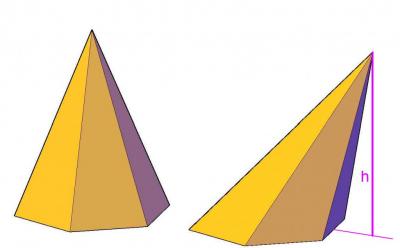
Видно, что помимо шестиугольника фигура состоит из шести треугольников, точка соединения которых называется вершиной. Различие между изображенными пирамидами заключается в том, что высота h правой из них не пересекает шестиугольное основание в его геометрическом центре, а высота левой фигуры попадает точно в этот центр. Благодаря этому критерию левая пирамида получила название прямой, а правая – наклонной.

Поскольку основание левой фигуры на рисунке образовано шестиугольником с равными сторонами и углами, то она называется правильной. Дальше в статье речь пойдет только об этой пирамиде.

Объем шестиугольной пирамиды

Для вычисления объема произвольной пирамиды справедлива следующая формула:

Здесь h – это длина высоты фигуры, S_o – площадь ее основания. Воспользуемся этим выражением для определения объема пирамиды шестиугольной правильной.

Поскольку в основании рассматриваемой фигуры лежит равносторонний шестиугольник, то для вычисления его площади можно воспользоваться следующим общим выражением для n-угольника:

S_n = n/4 * a 2 * ctg(pi/n)

Здесь n – целое число, равное количеству сторон (углов) многоугольника, a – длина его стороны, функцию котангенса высчитывают, используя соответствующие таблицы.

Применяя выражение для n = 6, получим:

S₆ = 6/4 * a 2 * ctg(pi/6) = √3/2 * a 2

Теперь остается подставить это выражение в общую формулу для объема V:

Таким образом, для вычисления объема рассматриваемой пирамиды необходимо знать два ее линейных параметра: длину стороны основания и высоту фигуры.

Пример решения задачи

Покажем, как можно использовать полученное выражение для V₆ для решения следующей задачи.

Известно, что правильной шестиугольной пирамиды объем равен 100 см 3 . Необходимо определить сторону основания и высоту фигуры, если известно, что они связаны друг с другом следующим равенством:

Поскольку в формулу для объема входят только a и h, то можно подставить в нее любой из этих параметров, выраженный через другой. Например, подставим a, получаем:

Для нахождения значения высоты фигуры необходимо взять корень третей степени из объема, что соответствует размерности длины. Подставляем значение объема V₆ пирамиды из условия задачи, получаем высоту:

h = ∛(100/(2*√3)) ≈ 3,0676 см

Поскольку сторона основания в соответствии с условием задачи в два раза больше найденной величины, то получаем значение для нее:

a = 2*h = 2*3,0676 = 6,1352 см

Объем шестиугольной пирамиды можно найти не только через высоту фигуры и значение стороны ее основания. Достаточно знать два разных линейных параметра пирамиды для его вычисления, например апотему и длину бокового ребра.

Объем правильной шестиугольной пирамиды 6. Формула объема шестиугольной пирамиды: пример решения задачи

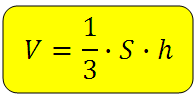
S – площадь основания пирамиды

h – высота пирамиды

Основанием может быть любой многоугольник. Но в большинстве задач на ЕГЭ речь в условии, как правило, идёт о правильных пирамидах. Напомню одно из её свойств:

Вершина правильной пирамиды проецируется в центр её основания

Посмотрите на проекцию правильной треугольной, четырёхугольной и шестиугольной пирамид (ВИД СВЕРХУ):

Можете посмотреть ещё одну статью на блоге, где разбирались задачи связанные с нахождением объёма пирамиды.

27087. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна корню из трёх.

Объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды

h – высота пирамиды

Найдём площадь основания пирамиды, это правильный треугольник. Воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Таким образом, объём пирамиды равен:

27088. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен корню из трёх.

Такие понятия как высота пирамиды и характеристики её основания связаны формулой объёма:

S – площадь основания пирамиды

h – высота пирамиды

Сам объём нам известен, площадь основания можем найти, так как известны стороны треугольника, который является основанием. Зная указанные величины без труда найдём высоту.

Для нахождения площади основания воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Таким образом, подставив данные значения в формулу объема можем вычислить высоту пирамиды:

Высота равна трём.

27109. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

Объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды

h – высота пирамиды

Высота нам известна. Необходимо найти площадь основания. Напомню, что вершина правильной пирамиды проецируется в центр её основания. Основанием правильной четырёхугольной пирамиды является квадрат. Мы можем найти его диагональ. Рассмотрим прямоугольный треугольник (выделен синим):

Отрезок соединяющий центр квадрата с точкой В это катет, который равен половине диагонали квадрата. Этот катет можем вычислить по теореме Пифагора:

Значит BD = 16. Вычислим площадь квадрата воспользовавшись формулой площади четырёхугольника:

Таким образом, объём пирамиды равен:

27178. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

Высота пирамиды и её и объём известны, значит можем найти площадь квадрата, который является основанием. Зная площадь квадрата, мы сможем найти его диагональ. Далее рассмотрев прямоугольный треугольник по теореме Пифагора вычислим боковое ребро:

Найдём площадь квадрата (основания пирамиды):

Вычислим диагональ квадрата. Так как его площадь равна 50, то сторона будет равна корню из пятидесяти и по теореме Пифагора:

Точка О делит диагональ BD пополам, значит катет прямоугольного треугольника ОВ = 5.

Таким образом, можем вычислить чему равно боковое ребро пирамиды:

245353. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

Как уже неоднократно было сказано – объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды

h – высота пирамиды

Боковое ребро перпендикулярное основанию равно трём, это означает, что высота пирамиды равна трём. Основания пирамиды – это многоугольник, площадь которого равна:

27086. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

27110. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60 0 . Высота пирамиды равна 6. Найдите объем пирамиды.

27111. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

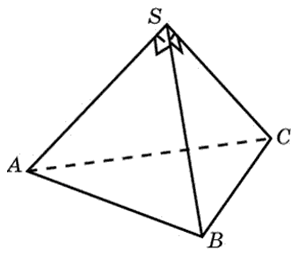
27113. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.

27114. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB . Найдите объем треугольной пирамиды EABC .

27176. Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.

27179. Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.

27181. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45 0 . Найдите объем пирамиды.

Источники:

http://autogear.ru/article/442/431/formula-obyema-shestiugolnoy-piramidyi-primer-resheniya-zadachi/
http://fb.ru/article/442431/formula-obyema-shestiugolnoy-piramidyi-primer-resheniya-zadachi
http://www.sites.google.com/site/110buldakova/ucebnye-kursy/stereometria/piramida/obem-piramidy