Формула суммы косинуса и синуса. Сумма и разность синусов и косинусов: вывод формул, примеры

Сумма и разность синусов и косинусов: вывод формул, примеры

Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α – β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.

Формулы суммы и разности синусов и косинусов

Запишем, как выглядят формулы суммы и разности для синусов и для косинусов

Формулы суммы и разности для синусов

sin α + sin β = 2 sin α + β 2 cos α – β 2 sin α – sin β = 2 sin α – β 2 cos α + β 2

cos α + cos β = 2 cos α + β 2 cos α – β 2 cos α – cos β = – 2 sin α + β 2 cos α – β 2 , cos α – cos β = 2 sin α + β 2 · β – α 2

Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α – β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.

Определения формул сумм и разности синусов и косинусов

Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.

Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.

Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.

Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.

Вывод формул суммы и разности синусов и косинусов

Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже

sin ( α + β ) = sin α · cos β + cos α · sin β sin ( α – β ) = sin α · cos β – cos α · sin β cos ( α + β ) = cos α · cos β – sin α · sin β cos ( α – β ) = cos α · cos β + sin α · sin β

Также представим сами углы в виде суммы полусумм и полуразностей.

α = α + β 2 + α – β 2 = α 2 + β 2 + α 2 – β 2 β = α + β 2 – α – β 2 = α 2 + β 2 – α 2 + β 2

Переходим непосредственно к выводу формул суммы и разности для sin и cos.

Вывод формулы суммы синусов

В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим

sin α + sin β = sin α + β 2 + α – β 2 + sin α + β 2 – α – β 2

Теперь к первому выражению применяем формулу сложения, а ко второму – формулу синуса разностей углов (см. формулы выше)

sin α + β 2 + α – β 2 = sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 sin α + β 2 – α – β 2 = sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 sin α + β 2 + α – β 2 + sin α + β 2 – α – β 2 = sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 + sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу

sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 + sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 = = 2 sin α + β 2 cos α – β 2

Действия по выводу остальных формул аналогичны.

Вывод формулы разности синусов

sin α – sin β = sin α + β 2 + α – β 2 – sin α + β 2 – α – β 2 sin α + β 2 + α – β 2 – sin α + β 2 – α – β 2 = sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 – sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 = = 2 sin α – β 2 cos α + β 2

Вывод формулы суммы косинусов

Вывод формулы разности косинусов

cos α – cos β = cos α + β 2 + α – β 2 – cos α + β 2 – α – β 2 cos α + β 2 + α – β 2 – cos α + β 2 – α – β 2 = cos α + β 2 cos α – β 2 – sin α + β 2 sin α – β 2 – cos α + β 2 cos α – β 2 + sin α + β 2 sin α – β 2 = = – 2 sin α + β 2 sin α – β 2

Примеры решения практических задач

Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.

Пример 1. Проверка формулы суммы синусов двух углов

α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 – π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2

Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.

Пример 2. Применение формулы разности синусов

α = 165 ° , β = 75 ° sin α – sin β = sin 165 ° – sin 75 ° sin 165 – sin 75 = 2 · sin 165 ° – 75 ° 2 cos 165 ° + 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · – 1 2 = 2 2

С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.

Тригонометрические формулы. Их вывод

Наиболее часто встречающиеся тригонометрические формулы:

(blacktriangleright) Основные тождества: [begin <|l|l|>hline sin^2 alpha+cos^2 alpha =1& mathrm, alpha cdot mathrm, alpha =1 \ &(sinalphane 0, cosalphane 0)\[0.5ex] hline &\ mathrm, alpha=dfrac &mathrm, alpha =dfrac \&\ 1+mathrm^2, alpha =dfrac1 & 1+mathrm^2, alpha=dfrac1\&\ (cosalphane 0)& (sinalphane 0) \ hline end]

(blacktriangleright) Формулы сложения углов: [begin <|l|r|>hline &\ sin<(alphapm beta)>=sinalphacdot cosbetapm sinbetacdot cosalpha & cos<(alphapm beta)>=cosalphacdot cosbeta mp sinalphacdot sinbeta\ &\ hline &\ mathrm, (alphapm beta)=dfrac, alphapm mathrm, beta><1 mp mathrm, alphacdot mathrm, beta> & mathrm, (alphapmbeta)=-dfrac<1mp mathrm, alphacdot mathrm, beta>, alphapm mathrm, beta>\&\ cosalphacosbetane 0&sinalphasinbetane 0\ hline end]

(blacktriangleright) Формулы двойного и тройного углов: [begin <|lc|cr|>hline sin <2alpha>=2sin alphacos alpha & qquad &qquad & cos<2alpha>=cos^2alpha -sin^2alpha\ sin alphacos alpha =dfrac12sin <2alpha>&& & cos<2alpha>=2cos^2alpha -1\ & & & cos<2alpha>=1-2sin^2 alpha\ hline &&&\ mathrm, 2alpha = dfrac<2mathrm, alpha><1-mathrm^2, alpha> && & mathrm, 2alpha = dfrac^2, alpha-1><2mathrm, alpha>\&&&\ cosalphane 0, cos2alphane 0 &&& sinalphane 0, sin2alphane 0\ hline &&&\ sin <3alpha>=3sin alpha -4sin^3alpha && & cos<3alpha>=4cos^3alpha -3cos alpha\&&&\ hline end]

(blacktriangleright) Формулы понижения степени: [begin <|lc|cr|>hline &&&\ sin^2alpha=dfrac<1-cos<2alpha>>2 &&& cos^2alpha=dfrac<1+cos<2alpha>>2\&&&\ hline end]

(blacktriangleright) Формулы произведения функций: [begin <|c|>hline \ sinalphasinbeta=dfrac12bigg(cos<(alpha-beta)>-cos<(alpha+beta)>bigg)\\ cosalphacosbeta=dfrac12bigg(cos<(alpha-beta)>+cos<(alpha+beta)>bigg)\\ sinalphacosbeta=dfrac12bigg(sin<(alpha-beta)>+sin<(alpha+beta)>bigg)\\ hline end]

(blacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [begin <|l|r|>hline &\ sin<2alpha>=dfrac<2mathrm, alpha><1+mathrm^2, alpha> & cos<2alpha>=dfrac<1-mathrm^2, alpha><1+mathrm^2, alpha>\&\ cosalphane 0 & sinalphane 0\ hline end]

(blacktriangleright) Формула вспомогательного аргумента: [begin <|c|>hline text<Частный случай>\ hline \ sinalphapm cosalpha=sqrt2cdot sin4right)>\\ sqrt3sinalphapm cosalpha=2sin6right)>\\ sinalphapm sqrt3cosalpha=2sin3right)>\\ hline text<Общий случай>\ hline\ asinalphapm bcosalpha=sqrtcdot sin<(alphapm phi)>, cosphi=dfrac a>, sinphi=dfrac b>\\ hline end]

Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.

Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.

(blacktriangleright) Вывод формулы косинуса разности углов (cos<(alpha -beta)>=cosalphacosbeta+sinalphasinbeta)

Рассмотрим тригонометрическую окружность и на ней углы (alpha) и (beta) . Пусть этим углам соответствуют точки (A) и (B) соответственно. Тогда координаты этих точек: (A(cosalpha;sinalpha), B(cosbeta;sinbeta)) .

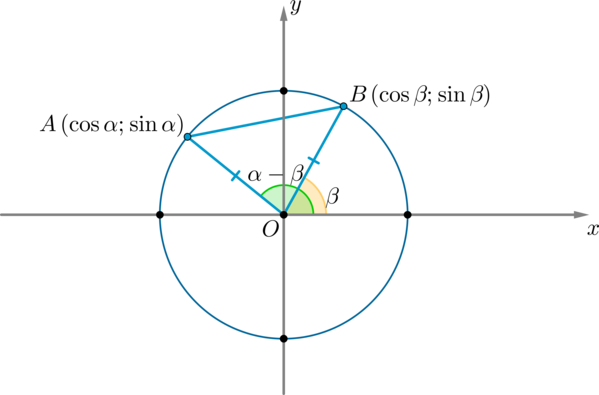
Рассмотрим (triangle AOB: angle AOB=alpha-beta) . По теореме косинусов:

(AB^2=AO^2+BO^2-2AOcdot BOcdot cos(alpha-beta)=1+1-2cos(alpha-beta) (1)) (т.к. (AO=BO=R) – радиус окружности)

По формуле расстояния между двумя точками на плоскости:

Таким образом, сравнивая равенства ((1)) и ((2)) :

Отсюда и получается наша формула.

(blacktriangleright) Вывод остальных формул суммы/разности углов:

Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения (sin x=cos(90^circ-x)) и (cos x=sin (90^circ-x)) :

разделим числитель и знаменатель дроби на (cosalphacosbetane 0)
(при (cosalpha=0 Rightarrow mathrm,(alphapmbeta)=mp mathrm,beta) , при (cosbeta=0 Rightarrow mathrm,(alphapmbeta)=pm mathrm,alpha) ):

Таким образом, данная формула верна только при (cosalphacosbetane 0) .

5) Аналогично, только делением на (sinalphasinbetane 0) , выводится формула котангенса суммы/разности двух углов.

(blacktriangleright) Вывод формул двойного и тройного углов:

Данные формулы выводятся с помощью предыдущих формул:

1) (sin 2alpha=sin(alpha+alpha)=sinalphacosalpha+sinalphacosalpha=2sinalphacosalpha)

Используя основное тригонометрическое тождество (sin^2alpha+cos^2alpha=1) , получим еще две формулы для косинуса двойного угла:

разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0 Rightarrow mathrm,2alpha=0) ):

Таким образом, эта формула верна только при (cosalphane 0) , а также при (cos2alphane 0) (чтобы существовал сам (mathrm,2alpha) ).

По тем же причинам при (sinalphane 0, sin2alphane 0) .

5) (sin3alpha=sin(alpha+2alpha)=sinalphacos2alpha+cosalphasin2alpha=sinalpha(1-2sin^2alpha)+cosalphacdot 2sinalphacosalpha=)

6) Аналогично выводится, что (cos3alpha=cos(alpha+2alpha)=4cos^3alpha-3cosalpha)

(blacktriangleright) Вывод формул понижения степени:

Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:

1) (cos2alpha=2cos^2alpha-1 Rightarrow cos^2alpha=dfrac<1+cos2alpha>2)

2) (cos2alpha=1-2sin^2alpha Rightarrow sin^2alpha=dfrac<1-cos2alpha>2)

Заметим, что в данных формулах степень синуса/косинуса равна (2) в левой части, а в правой части степень косинуса равна (1) .

(blacktriangleright) Вывод формул произведения функций:

1) Сложим формулы косинуса суммы и косинуса разности двух углов:

Получим: (cos(alpha+beta)+cos(alpha-beta)=2cosalphacosbeta Rightarrow cosalphacosbeta=dfrac12Big(cos(alpha-beta)+cos(alpha+beta)Big))

2) Если вычесть из формулы косинуса суммы косинус разности, то получим:

3) Сложим формулы синуса суммы и синуса разности двух углов:

(blacktriangleright) Вывод формул суммы/разности функций:

Обозначим (alpha+beta=x, alpha-beta=y) . Тогда: (alpha=dfrac2, beta=dfrac2) . Подставим эти значения в предыдущие три формулы:

Получили формулу суммы косинусов.

Получили формулу разности косинусов.

Получили формулу суммы синусов.

4) Формулу разности синусов можно вывести из формулы суммы синусов:

Аналогично выводится формула суммы котангенсов.

(blacktriangleright) Вывод формул выражения синуса и косинуса через тангенс половинного угла:

(разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0) и (sin2alpha=0) ):)

2) Так же, только делением на (sin^2alpha) , выводится формула для косинуса.

(blacktriangleright) Вывод формул вспомогательного угла:

Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.

Рассмотрим выражение (asin x+bcos x) . Домножим и разделим это выражение на (sqrt,) :

(asin x+bcos x=sqrtleft(dfrac a>sin x+ dfrac b>cos x right)=sqrtbig(a_1sin x+b_1cos xbig))

Заметим, что таким образом мы добились того, что (a_1^2+b_1^2=1) , т.к. (left(dfrac a>right)^2+left(dfrac b>right)^2=dfrac=1)

Таким образом, можно утверждать, что существует такой угол (phi) , для которого, например, (cos phi=a_1, sin phi=b_1) . Тогда наше выражение примет вид:

(sqrt,big(cos phi sin x+sin phicos xbig)=sqrt,sin (x+phi)) (по формуле синуса суммы двух углов)

Значит, формула выглядит следующим образом: [,sin (x+phi),>> quad text <где >cos phi=dfrac a>] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt,cos (x-phi)]

(blacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла:

(a) sin xpmcos x=sqrt2,left(dfrac1sin xpmdfrac1cos xright)=sqrt2, sin left(xpmdfrac4right))

(b) sqrt3sin xpmcos x=2left(dfrac2sin xpm dfrac12cos xright)=2, sin left(xpmdfrac6right))

(c) sin xpmsqrt3cos x=2left(dfrac12sin xpmdfrac2cos xright)=2,sinleft(xpmdfrac3right))

Синус суммы углов вывод формулы. Сумма и разность синусов и косинусов: вывод формул, примеры

Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α – β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.

Формулы суммы и разности синусов и косинусов

Запишем, как выглядят формулы суммы и разности для синусов и для косинусов

Формулы суммы и разности для синусов

sin α + sin β = 2 sin α + β 2 cos α – β 2 sin α – sin β = 2 sin α – β 2 cos α + β 2

Формулы суммы и разности для косинусов

cos α + cos β = 2 cos α + β 2 cos α – β 2 cos α – cos β = – 2 sin α + β 2 cos α – β 2 , cos α – cos β = 2 sin α + β 2 · β – α 2

Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α – β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.

Определения формул сумм и разности синусов и косинусов

Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.

Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.

Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.

Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.

Вывод формул суммы и разности синусов и косинусов

Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже

sin (α + β) = sin α · cos β + cos α · sin β sin (α – β) = sin α · cos β – cos α · sin β cos (α + β) = cos α · cos β – sin α · sin β cos (α – β) = cos α · cos β + sin α · sin β

Также представим сами углы в виде суммы полусумм и полуразностей.

α = α + β 2 + α – β 2 = α 2 + β 2 + α 2 – β 2 β = α + β 2 – α – β 2 = α 2 + β 2 – α 2 + β 2

Переходим непосредственно к выводу формул суммы и разности для sin и cos.

Вывод формулы суммы синусов

В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим

sin α + sin β = sin α + β 2 + α – β 2 + sin α + β 2 – α – β 2

Теперь к первому выражению применяем формулу сложения, а ко второму – формулу синуса разностей углов (см. формулы выше)

sin α + β 2 + α – β 2 = sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 sin α + β 2 – α – β 2 = sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 sin α + β 2 + α – β 2 + sin α + β 2 – α – β 2 = sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 + sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу

sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 + sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 = = 2 sin α + β 2 cos α – β 2

Действия по выводу остальных формул аналогичны.

Вывод формулы разности синусов

sin α – sin β = sin α + β 2 + α – β 2 – sin α + β 2 – α – β 2 sin α + β 2 + α – β 2 – sin α + β 2 – α – β 2 = sin α + β 2 cos α – β 2 + cos α + β 2 sin α – β 2 – sin α + β 2 cos α – β 2 – cos α + β 2 sin α – β 2 = = 2 sin α – β 2 cos α + β 2

Вывод формулы суммы косинусов

cos α + cos β = cos α + β 2 + α – β 2 + cos α + β 2 – α – β 2 cos α + β 2 + α – β 2 + cos α + β 2 – α – β 2 = cos α + β 2 cos α – β 2 – sin α + β 2 sin α – β 2 + cos α + β 2 cos α – β 2 + sin α + β 2 sin α – β 2 = = 2 cos α + β 2 cos α – β 2

Вывод формулы разности косинусов

cos α – cos β = cos α + β 2 + α – β 2 – cos α + β 2 – α – β 2 cos α + β 2 + α – β 2 – cos α + β 2 – α – β 2 = cos α + β 2 cos α – β 2 – sin α + β 2 sin α – β 2 – cos α + β 2 cos α – β 2 + sin α + β 2 sin α – β 2 = = – 2 sin α + β 2 sin α – β 2

Примеры решения практических задач

Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.

Пример 1. Проверка формулы суммы синусов двух углов

α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 – π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2

Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.

Пример 2. Применение формулы разности синусов

α = 165 ° , β = 75 ° sin α – sin β = sin 165 ° – sin 75 ° sin 165 – sin 75 = 2 · sin 165 ° – sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · – 1 2 = 2 2

С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Косинус суммы и разности двух углов

В этом параграфе будут доказаны следующие две формулы:

cos (α + β) = cos α cos β – sin α sin β, (1)

cos (α – β) = cos α cos β + sin α sin β. (2)

Косинус суммы (разности) двух углов равен произведению косинусов этих углов минус (плюс) произведение синусов этих углов.

Нам удобнее будет начать с доказательства формулы (2). Для простоты изложения предположим сначала, что углы α и β удовлетворяют следующим условиям:

1) каждый из этих углов неотрицателен и меньше 2π :

Пусть положительная часть оси 0х является общей начальной стороной углов α и β .

Конечные стороны этих углов обозначим соответственно через 0А и 0В. Очевидно, что угол α – β можно рассматривать как такой угол, на который нужно повернуть луч 0В вокруг точки 0 против часовой стрелки, чтобы его направление совпало с направлением луча 0А.

На лучах 0А и 0В отметим точки М и N, отстоящие от начала координат 0 на расстоянии 1, так что 0М = 0N = 1.

В системе координат х0у точка М имеет координаты (cos α, sin α ), а точка N – координаты (cos β , sin β ). Поэтому квадрат расстояния между ними равен:

d 1 2 = (cos α – cos β) 2 + (sin α – sin β) 2 = cos 2 α – 2 cos α cos β +

+ cos 2 β + sin 2 α – 2sin α sin β + sin 2 β = .

При вычислениях мы воспользовались тождеством

sin 2 φ + cos 2 φ = 1 .

Теперь рассмотрим другую систему координат В0С, которая получается путем поворота осей 0х и 0у вокруг точки 0 против часовой стрелки на угол β .

В этой системе координат точка М имеет координаты (cos (α – β ), sin (α – β )), а точка N -координаты (1,0). Поэтому квадрат расстояния между ними равен:

d 2 2 = 2 + 2 = cos 2 (α – β) – 2 cos (α – β) + 1 +

Но расстояние между точками М и N не зависит от того, относительно какой системы координат мы рассматриваем эти точки. Поэтому

2 (1 – cos α cos β – sin α sin β) = 2 .

Отсюда и вытекает формула (2).

Теперь следует вспомнить о тех двух ограничениях, которые мы наложили для простоты изложения на углы α и β .

Требование, чтобы каждый из углов α и β был неотрицательным, на самом деле не существенно. Ведь к любому из этих углов можно прибавить угол, кратный 2я, что никак не отразится на справедливости формулы (2). Точно так же от каждого из данных углов можно вычесть угол, кратный 2π . Поэтому можно считать, что 0 β . Действительно, если α α ; поэтому, учитывая четность функции cos х , получаем:

cos (α – β) = cos (β – α) = cos β cos α + sin β sin α,

что по существу совпадает с формулой (2). Таким образом, формула

cos (α – β) = cos α cos β + sin α sin β

верна для любых углов α и β . В частности, заменяя в ней β на –β и учитывая, что функция cos х является четной, а функция sin х нечетной, получаем:

cos (α + β) = cos [α – (- β)] =cos α cos (-β) + sin α sin (-β) =

= cos α cos β – sin α sin β,

что доказывает формулу (1).

Итак, формулы (1) и (2) доказаны.

1) cos 75° = cos (30° + 45°) = cos 30° cos 45°-sin 30°-sin 45° =

2) cos 15° = cos (45° – 30°) = cos 45° cos 30° + sin 45° sin 30° =

1 . Вычислить, не пользуясь тригонометрическими таблицами:

a) cos 17° cos 43° – sin 17° sin 43°;

б) sin 3° sin 42° – cos 39° cos 42°;

в) cos 29° cos 74° + sin 29° sin 74°;

г) sin 97° sin 37° + cos 37° cos 97°;

д) cos 3π / 8 cos π / 8 + sin 3π / 8 sin π / 8 ;

e) sin 3π / 5 sin 7π / 5 – cos 3π / 5 cos 7π / 5 .

a). cos (α + π / 3 ) + cos (π / 3 – α ) .

б). cos (36° + α ) cos (24° – α ) + sin (36° + α ) sin (α – 24°).

в). sin (π / 4 – α ) sin (π / 4 + α ) – cos (π / 4 + α ) cos (π / 4 – α )

a) cos (α – β) , если

cos α = – 2 / 5 , sin β = – 5 / 13 ;

Источники:

http://zaochnik.com/spravochnik/matematika/trigonometrija/summa-i-raznost-sinusov-i-kosinusov/
http://shkolkovo.net/theory/26
http://araratpark-hyatt.ru/sinus-summy-uglov-vyvod-formuly-summa-i-raznost-sinusov-i-kosinusov-vyvod.html